99% Disappointing

When I first heard there was an antibody (serum) test I thought wow, this is fantastic!  If you are certified to have already had it, then you know that it’s safe for you to be around others and others can be confident that they are safe around you. It could be like a license to go to work.

Then I thought about it.  Actually, the test is probably useless for you, personally. (It has other uses, like making policy, but that’s not what we’re talking about here.) The problem has nothing to do with not knowing whether Covid-19 guarantees future immunity. You don’t need to go there in order to show that it’s useless for the average person.

This isn’t an Internet crackpot thing—it’s real math you can verify yourself.  It’s a disappointment but the reasons are interesting and the principle applies to all tests that yield a positive/negative result. The smaller the proportion of people in the population that have the condition in question, the more this principle applies.

I’m just going to explain one small aspect of this. One of the main places this applies is in diagnosing illnesses and that water gets very deep. Still, it’s interesting to poke around in it and it might help you understand what your doctor is doing someday.

What Does 99% Accurate Mean?

For at least two intertwined reasons, it doesn’t mean anything to say that a test is x% accurate. Any claim offering a single percentage value is just muddying the water. The first reason is that tests like this have two different kinds of accuracy: the probability that a positive result is true and the probability that a negative result is true. They mean completely different things and the two probabilities are very often different for the same test.

The paradox is that even if a test is 99% accurate with respect to positive results, the probability that a random person’s positive result is false can still be very high. In fact, in many realistic scenarios with Covid-19, a positive result is more likely to be false than true.

That may seem to be self-contradictory, but it’s not. Unlike normal humans, statisticians and lawyers say precisely what they mean. Most of the rest of us just aren’t used to it.   You have to understand a couple of things before it is clear what 99% accurate means.

Sensitivity v Specificity

The first kind of accuracy is called “sensitivity.” On average, when you test 100 people who are known to have a certain condition using a test with a sensitivity of 99%, 99 of them will test positive for it. That’s what it means. It sounds simple but the catch is that a sensitive test can also flag any number of additional people who really don’t have it.  A sensitive test rarely gives a false negative result but it is allowed to give false positives galore.

The second kind of accuracy is “specificity.”  If a test has a specificity of 99%, on average, every time you test 100 people who definitely do not have the disease, no more than 1% of them will test positive. The catch is, the test can give any percentage of false negatives.

So what you ideally want is a test that scores high both ways.  Sensitivity insures that a test is positive for most people that have a condition and specificity rules out most of the false positives that sensitivity permits for people who don’t really have it.

Sensitivity and specificity aren’t all or nothing, of course. A test has a sensitivity of X% and a specificity of Y% and it is not unusual for a test to be strong on one and weak on the other.  Tests that are weak in one or the other still have uses. For instance, if a doctor is trying to diagnose an illness, a test with high sensitivity and low specificity can rule out a condition even though it can’t reliably say that a person has it. A test with low sensitivity but high specificity can tell you the patient very likely has the disease because it’s good about false positives but it can’t tell you that they don’t have it because it’s allowed to show false negatives. I.e., you can rule things in but not out.

The Covid-19 antibody tests are actually pretty good both ways. The one called the Celex test has a sensitivity of 94% and a specificity of 96%.

That’s a Relief!

So if you give 1000 people who had Covid-19 the Celex test, 940 of them will test positive. And if you give 1000 people who’ve never had Covid-19 the Celex test, 960 of them will test negative.  I thought you said the tests were useless?

I’m sticking with that opinion. Read on.

The Catch

It’s not a paradox, just simple math. Let’s take an exaggerated case to make the reason for it clear.

Imagine a hideous disease that only one person in a million has. You’re a nervous hypochondriac with no symptoms of the disease but you have insomnia from worrying about it. Fortunately there’s a test with 99% sensitivity and 99% specificity so you decide to get tested so you can rest easy.

Unfortunately, the test comes back positive. Is it time to join the Hemlock Society Web Forum?

Not at all. Even if you get a positive result it’s hardly worth worrying about.  It’s like this.

It’s a one in a million disease and there are 325,000,000 people in the USA, so 325 people actually have it.  Now, imagine that you tested all 325 million Americans. The test is 99% specific so only 1% of people get false positives but that’s still 3,249,625 false positives plus 322 true positives (3 of the 325 people who really had it got false negative results.) Call it 3.25 million positive results.

The number who actually have it, 325, divided by the number of people who come back positive, 3,250,00, is 0.0001. One in ten thousand positive results is actually true. That’s worse than scratch-off card odds.

In other words, even with a positive test result, the chance that you have the disease is about the same as the chance that you’ll die in a car wreck this year.  So be sure to only take the subway this year and you should be fine. (That’s a statistics joke.)

The same principle works for false negatives but you get a very different result because out of 325 million tests only 325 people even have a chance of a false negative and only 1% of them will get one. 1% of people who have the disease will get a false negative but for a random person, the chance that a negative result is wrong is a million, which is lottery odds.

Qualifying the Percentage

Statistics people will usually specify both the sensitivity and the specificity.  To give a single number for “accuracy” you would have to say which one you mean (false positive or false negative) in the context of some specific density of cases in the population. 

You will see this in the chart below.

Getting Specific to Covid-19

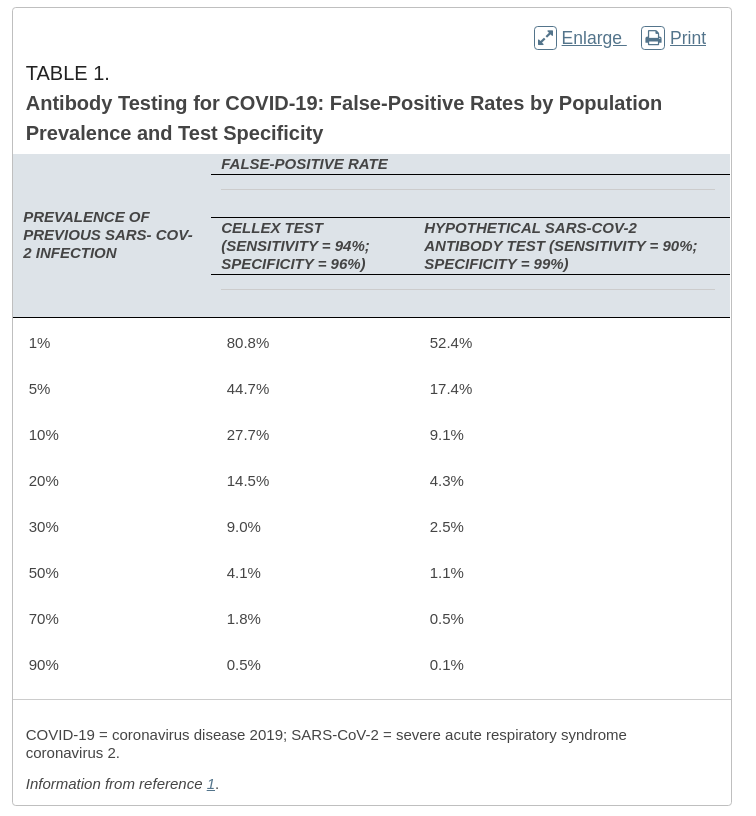
Here’s a chart from an letter published in American Family Physician  specifically about the probability of false positives that you’d see from the actual Cellex antibody test for Covid-19 given a wide range of hypothetical densities of people who have actually had Covid-19. The author worked these out, but you can reproduce similar numbers yourself using an Excel spreadsheet for any given sensitivity, specificity, and range of population densities.

Nobody knows what the real number of people in the US who’ve had Covid-19 is. The number of confirmed cases as of today (July 17 2020) is around 3.5 million, which is a little more than 1% but the real number is surely higher. Let’s say the real number is more like 5%, i.e., out of every five that got it, only one was confirmed.  It’s very hard to get a straight answer about this ratio from any source, BTW. I’ve seen estimates from 2X to 15X. This recent Washington Post article cites the head of the CDC estimating 10x for the USA in June, but testing for active Covid-19 has ramped up rapidly lately so that estimate could be unrealistically high by now.

Whatever the number, even if it is accurate, it is unlikely to be correct for your particular town of area for reasons I’ll explain below.

Looking at the chart below, if the multiplier is 5X, which gives a density of about 5% in the population, so if a randomly selected person takes the test and gets a positive result for antibodies, the result will be wrong 44% of the time (because the false positive rate for the 95% of people we are assuming have not had Covid-19.)

Even with the hypothetical better test that yields only 1% false positives, if only 5% of the population actually had Covid-10 it, a positive test would still be wrong 17.4% of the time.

If you think the CDC Director’s estimate that I mentioned above is more trustworthy, use 10X, which still yields 27.7% false positives and 9.1% false positives, respectively for the two tests.  It’s not impressively accurate either way and the second test doesn’t really exist.

It’s Worse Than It Sounds

Whatever the real density of cases in the population of the USA is, it would tend to overestimate the case density for the majority of towns and cities because the hot spots are accounting for disproportionately many of the USA’s cases.  That’s why the letter emphasizes local conditions.

For instance, New York City, one of the hardest hit places in the country, makes up about 2.8% of the USA population but had about 225,000 confirmed cases or 6.25% of cases to date. It used to be a higher percentage but new cases are way down in NYC and up elsewhere. There are eight million New Yorkers, so about 2.8% of New Yorkers were confirmed to have had it at some point. If the real number is five times the number of confirmed cases then about 14% of New Yorkers have had it.

Crudely interpolating from the chart we see that under the 5X assumption, somewhere between 20% and 60% of positive antibody tests will be false.  If the real multiple is 10x, then 28% of New Yorkers have had it (which I find implausible) and you get 9% false positives.

The reason that 10X is probably too high a multiple for NYC is that NY one of the states with the lowest percentage of positive results for tests for the illness (1.4%). NYC does a lot of testing. This tells you that NYC is almost certainly confirming a higher than average percentage of the actual cases and therefore the confirmed case count and actual case count will be closer together. In contrast, Arizona has about 21% positives, so by the same reasoning, they are probably failing to confirm a higher than average percentage.

So What Does This Mean Practically?

The letter from which the chart is taken is typical of the blandness of the commentary one reads on this subject. It makes great sense to advise doctors to consider local prevalence of Covid-19 in order to estimate the probability of a false positive, but it seems almost perverse, not to point out that there is currently nowhere in the entire country where the density of cases is high enough to make it probably that a positive test result for a random person is probably a true positive.

It is an academic/professional convention to say things in the blandest possible way and leave the reader to draw the right conclusion. I get that, but in this case, the reason for publishing the letter is that the prior expectation is that the reader will have failed to draw the first conclusion on their own.

I wonder how many doctors even understand the math well enough to draw the correct conclusions?  Some diagnosticians do, but I suspect that most doctors use tests almost as naively as we civilians do. This is because, in many case, when doctors prescribe a test, it is to people they already strongly suspect have the condition being tested for.  When this is the case, the density of people who have the condition is likely to be fairly high, and therefore, false positive results are relatively close to the sensitivity score.

In the current situation, you have two distinct groups: people who are getting the test because they suddenly lost their sense of small and got a bad cough, and another large group of people who are essentially being tested randomly.

In the former situation, the true positive rate will be reasonably close to the sensitivity rate, but in the latter case, it will more like what is described in the doctor’s letter above.

For this reason, you could argue that very little about testing lines up with how we interpret them.  Say the specificity is 95%–out of a classroom of 30 kids, it is likely that one would test positive even if nobody has it!  Even if it’s 99%, among three classrooms it’s more or less a coin flip.

It is equally odd to not mention that even if the density were high enough, we’d have no way of knowing because we don’t do enough random testing to generate the hypothetical locally specific estimates the use which is central to the author’s advice.

Conclusions

False positives are a nuisance to the few people who are unnecessarily kept home and isolated when they weren’t actually infected, but from society’s point of view, who cares if a few extra people have to stay home watching Netfix? You still filter out almost all the people who have it.

With false negatives it’s the opposite. They don’t greatly harm the person taking the test, who has it either way, but they are terrible from society’s point of view, as a person who falsely believes they don’t have it feels licensed to mingle with the uninfected.

So clearly, the value of the tests depends on one’s perspective but happily, it works out for the best either way. From the point of the individual, it’s the negative you want, and it’s the negative that can be most relied upon.  For society, it’s the true positives that are important, and even though false positives are common, they aren’t very important from the point of view of keeping people safe.

Even if Covid-19 is very rare where you live, making the probability that your positive test is false quite high, one never ignores a positive result even if it’s probably false. Remember, it may be unlikely that you have it, but statistically, they are filtering out almost everyone who does have it, keeping them home.

Disclaimer

I hope it is needless to say, but let’s be clear that this isn’t medical advice. If this makes things clearer, great, but it’s not a basis for second guessing the doctor or the CDC. The main point is, think critically. Remember that claims of accuracy expressed as a single number are misleading or outright false 100% of the time because there’s no such thing.  Even if both sensitivity as specificity are given, the numbers still may not mean much if you don’t know the prevalence of cases in the population being tested.  While you’re doing the math, be sure to wear your mask.